The Intel Math Kernel Library (MKL) contains a collection of highly optimized numerical functions.  Among others, it provides implementations of Blas functions and Lapack functions for various linear algebra problems.

A program, which is dynamically linked against the standard Blas and Lapack libraries, can easily benefit from alternative optimized implementations by replacing libblas.so and liblapack.so by optimized variants.  The MKL, however, does not come with a drop-in replacement for libblas.so and liblapack.so. But it comes with a tool for building such drop-in replacements.

The MKL is shipped with the Intel® Parallel Studio XE and with the Intel® System Studio.  The directory mkl/tools/builders under the installation directory of Intel® Parallel Studio XE and the Intel® System Studio contains a makefile to build libblas.so and liblapack.so on the basis of the MKL.  I found it appropriate to tweak this makefile for better compatibility.

• Replace “IFACE_COMP_PART=intel” by “IFACE_COMP_PART=gf”.
• Replace “IFACE_THREADING_PART=intel” by “IFACE_THREADING_PART=gnu”.
• Replace “LIBM=-lm” by “LIBM=-lm -mkl”.
• Replace all occurrences of “gcc” by “icc”.

With these little changes

# make libintel64 interface=lp64 export=blas_example_list name=libblas

and

# make libintel64 interface=lp64 export=lapack_example_list name=liblapack


will build new libblas.so and liblapack.so.  Now, one could overwrite the system’s libblas.so (and libblas.so.3) and liblapack.so (and liblapack.so.3) by the new version and all dynamically linked programs would benefit from the optimized libraries.  On Debian-based systems, however, one should use the alternatives mechanism instead.  This allows to switch easily between different Blas and Lapack implementations.  The following commands add the optimized libraries and make them the default choice (paths may differ on different Linux installations):

# update-alternatives --install /usr/lib/libblas.so libblas.so /usr/local/intel/mkl/tools/builder/libblas.so 800
# update-alternatives --install /usr/lib/libblas.so.3 libblas.so.3 /usr/local/intel/mkl/tools/builder/libblas.so 800
# update-alternatives --install /usr/lib/liblapack.so liblapack.so /usr/local/intel/mkl/tools/builder/liblapack.so 800
# update-alternatives --install /usr/lib/liblapack.so.3 liblapack.so.3 /usr/local/intel/mkl/tools/builder/liblapack.so 800

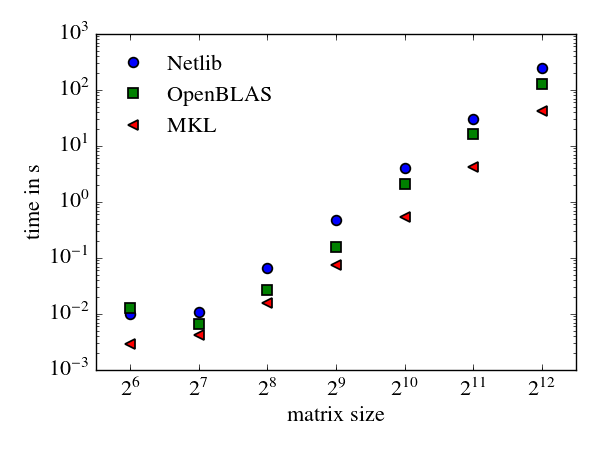
To test the effect of various Blas and Lapack implementations I wrote a small python script, which calculates the eigenvalues of Hermitian matrices of varying size.  Depending of the chosen Blas and Lapack implementations this more than an order of magnitude faster.  The Netlib reference implementation of Blas and Lapack is rather slow.  OpenBlas is much faster than Netlib, but the MKL is even faster.  Both are able to take advantage of multi-core architectures, which explains partly the performance boost.

#!/usr/bin/env python
# -*- coding: utf-8 -*-

# compatibility for Python 3
from __future__ import absolute_import, division, print_function
from pylab import *
import timeit

T=timeit.default_timer

sizes=array([64, 128, 256, 512, 1024, 2048, 4096])
times=list()
for N in sizes:
    A=randn(N, N)+1j*rand(N, N)
    A=A+A.conj().T
    start=T()
    eigh(A)
    end=T()
    times.append(end-start)
    print(N, end-start)
times=array(times)
savetxt('bench.dat', vstack((sizes, times)).T, fmt='%i\t%g')

Benchmark results for the code shown above on an Intel(R) Core(TM) i7-4500U CPU @ 1.80GHz (dual core CPU) with various Blas and Lapack implementations.