In a recent project (the numerical solution of the Dirac equation) I am working on, the computation of the fast Fourier transform (FFT) of four interwoven two-dimensional grids is the main computational task. Interwoven grids means that the memory layout of the matrices is such that data starts with the 1st element of the 1st matrix followed by the 1st element of the 2nd, 3rd and 4th matrix, respectively. The 5th data element represents the 2nd element of the 1st matrix and so on.
I tested two different FFT libraries that are able to compute a FFT in parallel on shared memory computers, the FFTW (version 3.2.2) and the Intel® MKL (the version that comes with the Intel® compiler suite version 11.1.056), and was quite surprised to see very large performance differences for this particular kind of parallel FFT. The Intel® MKL FFT routines show a very poor parallel speedup. Even with eight cores, the speedup never exceeds two, whereas the FFTW library reaches a reasonable speedup.
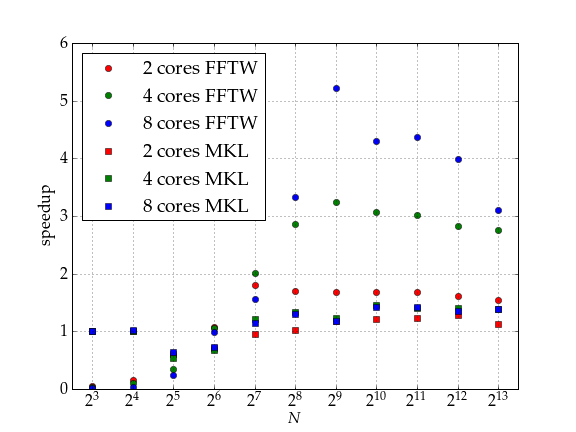
The FFTW library also excels the MKL in terms of absolute computing time. Depending on the problem size, FFTW may be four times faster. Only for very small matrices, the MKL is superior. Thus, one my conclude that the FFTW library is a good example how a high quality open source software can outperform a vendor library.
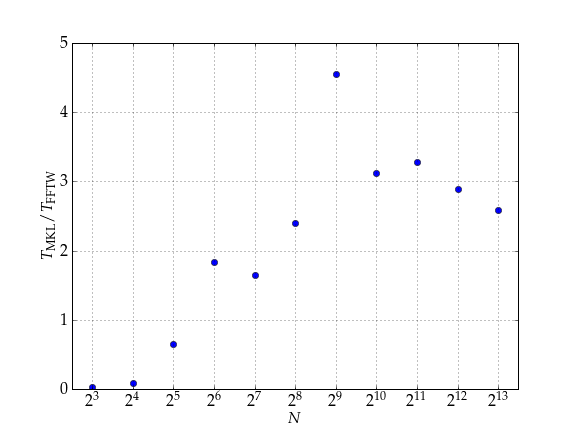
All performance measurements have been done on a system with two Quad Core Intel® Xeon® CPUs (E5345) at 2.5GHz. FFT plans were generated in measure mode. It would be very interesting for me to do a similar FFT benchmark on graphics hardware. However, I do not own a high performance graphics card.
Update: My test program utilized a lightweight convenience wrapper around FFTW (and the MKL internal FFTW-wrapper). For this reason I do not want to publish the original code. However, here is an equivalent program that does not depend on external libraries except FFTW.
// depending on your compiler and os compile with
//
// g++ -fopenmp -O3 -o time_dirac_fft time_dirac_fft.cc -lfftw3 -lfftw3_threads -pthread
//
// or with
//
// icc -openmp -O3 -o time_dirac_fft time_dirac_fft.cc -lmkl_intel -lmkl_intel_thread -lmkl_core
//
// or with
//
// icc -openmp -O3 -o time_dirac_fft time_dirac_fft.cc -lmkl_intel_lp64 -lmkl_intel_thread -lmkl_core
#include <cstdlib>
#include <complex>
#include <iostream>
#include <sstream>
#include <fstream>
#include <omp.h>
#include <fftw3.h>
#if defined __unix__
#include <unistd.h>
#include <sys/time.h>
#include <sys/times.h>
#else
#include <ctime>
#endif
// helper class for time measurements
class timer {
private:
const double _resolution;
double _t, _t_start;
bool isrunning;
double get_time() const {
#if defined __unix__
struct timeval tv;
gettimeofday(&tv, 0);
return static_cast<double>(tv.tv_sec)+static_cast<double>(tv.tv_usec)*1e-6;
#else
return static_cast<double>(std::clock())*_resolution;
#endif
}
public:
void reset() {
_t=0.0;
}
void start() {
_t_start=get_time();
isrunning=true;
}
void stop() {
if (isrunning) {
_t+=get_time()-_t_start;
isrunning=false;
}
}
double time() const {
return _t+( isrunning ? get_time()-_t_start : 0.0 );
}
double resolution() const {
return _resolution;
};
timer() :
#if defined __unix__
_resolution(1e-6),
#else
_resolution(1.0/CLOCKS_PER_SEC),
#endif
_t(0), _t_start(get_time()),
isrunning(true) {
}
};
typedef std::complex<double> complex;
// test FFT performance as required for one-dimensional Dirac equation
void time_1d(int p, std::ostream &out) {
out << "% one dimensional FFT\n"
<< "% two grids interwoven\n"
<< "%\n"
<< "% number of cpus = " << p << "\n"
<< "%\n"
<< "% n\ttime in sec.\n";
omp_set_num_threads(p);
omp_set_dynamic(false);
fftw_plan_with_nthreads(p);
for (int n=4; n<=16777216; n*=2) {
complex *v=reinterpret_cast<complex *>(fftw_malloc(2*n*sizeof(*v)));
if (v!=0) {
fftw_iodim io_n[1]={ {n, 2, 2} };
fftw_iodim io_is[1]={ {2, 1, 1} };
fftw_plan p1=fftw_plan_guru_dft(1, io_n, 1, io_is,
reinterpret_cast<fftw_complex *>(v),
reinterpret_cast<fftw_complex *>(v),
FFTW_FORWARD, FFTW_MEASURE);
fftw_plan p2=fftw_plan_guru_dft(1, io_n, 1, io_is,
reinterpret_cast<fftw_complex *>(v),
reinterpret_cast<fftw_complex *>(v),
FFTW_BACKWARD, FFTW_MEASURE);
for (int i=0; i<n; ++i) {
v[2*i]=complex(static_cast<double>(i+1)/static_cast<double>(n),
static_cast<double>(i+1)/static_cast<double>(n));
v[2*i+1]=complex(static_cast<double>(i+1)/static_cast<double>(n),
static_cast<double>(i+1)/static_cast<double>(n));
}
timer T1;
T1.start();
int i=0;
do {
fftw_execute_dft(p1,
reinterpret_cast<fftw_complex *>(v),
reinterpret_cast<fftw_complex *>(v));
fftw_execute_dft(p2,
reinterpret_cast<fftw_complex *>(v),
reinterpret_cast<fftw_complex *>(v));
++i;
} while (T1.time()<4 and i<16);
double t1=T1.time()/i;
fftw_free(v);
fftw_destroy_plan(p1);
fftw_destroy_plan(p2);
out << n << '\t' << t1 << std::endl;
std::cerr << "1d\tp = " << p
<< "\tN = " << n
<< "\ttime = " << t1 << std::endl;
} else
std::cerr << "2d\tp = " << p
<< "\tN = " << n
<< "\tnot enough memory" << std::endl;
}
}
// test FFT performance as required for two-dimensional Dirac equation
void time_2d(int p, std::ostream &out) {
out << "% two dimensional FFT\n"
<< "% four grids interwoven\n"
<< "%\n"
<< "% number of cpus = " << p << "\n"
<< "%\n"
<< "% n\ttime in sec.\n";
omp_set_num_threads(p);
omp_set_dynamic(false);
fftw_plan_with_nthreads(p);
for (int n=4; n<=8192; n*=2) {
complex *v=reinterpret_cast<complex *>(fftw_malloc(4*n*n*sizeof(*v)));
if (v!=0) {
fftw_iodim io_n[2]={ {n, 4, 4}, {n, 4*n, 4*n} };
fftw_iodim io_is[1]={ {4, 1, 1} };
fftw_plan p1=fftw_plan_guru_dft(2, io_n, 1, io_is,
reinterpret_cast<fftw_complex *>(v),
reinterpret_cast<fftw_complex *>(v),
FFTW_FORWARD, FFTW_MEASURE);
fftw_plan p2=fftw_plan_guru_dft(2, io_n, 1, io_is,
reinterpret_cast<fftw_complex *>(v),
reinterpret_cast<fftw_complex *>(v),
FFTW_BACKWARD, FFTW_MEASURE);
for (int j=0; j<n; ++j)
for (int i=0; i<n; ++i) {
v[4*(j*n+i)]=complex(static_cast<double>(i+1)/static_cast<double>(n),
static_cast<double>(j+1)/static_cast<double>(n));
v[4*(j*n+i)+1]=complex(static_cast<double>(i+1)/static_cast<double>(n),
static_cast<double>(j+1)/static_cast<double>(n));
v[4*(j*n+i)+2]=complex(static_cast<double>(i+1)/static_cast<double>(n),
static_cast<double>(j+1)/static_cast<double>(n));
v[4*(j*n+i)+3]=complex(static_cast<double>(i+1)/static_cast<double>(n),
static_cast<double>(j+1)/static_cast<double>(n));
}
timer T1;
T1.start();
int i=0;
do {
fftw_execute_dft(p1,
reinterpret_cast<fftw_complex *>(v),
reinterpret_cast<fftw_complex *>(v));
fftw_execute_dft(p2,
reinterpret_cast<fftw_complex *>(v),
reinterpret_cast<fftw_complex *>(v));
++i;
} while (T1.time()<4 and i<16);
double t1=T1.time()/i;
fftw_free(v);
fftw_destroy_plan(p1);
fftw_destroy_plan(p2);
out << n << '\t' << t1 << std::endl;
std::cerr << "2d\tp = " << p
<< "\tN = " << n
<< "\ttime = " << t1 << std::endl;
} else
std::cerr << "2d\tp = " << p
<< "\tN = " << n
<< "\tnot enough memory" << std::endl;
}
}
int main() {
fftw_init_threads();
for (int p=1; p<=8; ++p) {
{
std::stringstream name;
name << "fftw_timing_dirac_1d_p=" << p << ".dat";
std::ofstream out(name.str().c_str());
time_1d(p, out);
}
{
std::stringstream name;
name << "fftw_timing_dirac_2d_p=" << p << ".dat";
std::ofstream out(name.str().c_str());
time_2d(p, out);
}
}
return EXIT_SUCCESS;
}
Hi,
Is it possible to see sources of your both benchmarks: for using FFTW and MKL?
Or MKL was run via MKL internal FFTW-wrappers on the same benchmark….
— Thanks
I updated my post incorporating the source code of a test program.
Hi.
Very interesting the post. I am doing the same but for a different application. The point is that I am not able to reproduce your results (thank s for posting the code ) and I have realised that the problem has to be in the way I compile fftw. Reading the manual I only write
./configure –enable-openmp
Then to compile the application I use your compile line. The code runs on different processors but I don’t get quicker results. Example, for the 2d case (1024×1024) I get
p=1 time = 0.449826
p=2 time = 0.457931
p=4 time = 0.528959
p=8 time = 0.675827
Weird, isn’t it?
Weird, indeed. Parallel FFT performance depends considerably on the computer’s memory bandwidth. On my laptop with an Intel(R) Core(TM)2 Duo CPU, for example, I get virtually no speedup using two threads. However, I compiled my version of the FFTW library with the option
--enable-threads. Maybe, you should try this option instead of-–enable-openmp.Hi.
I am doing a similar work but using 3D fft’s. And i have some different/interesting results, that i would like to discuss with you.
The speedup of the FFTW Library is great (linear on most of the sizes used), when comparing with the MKL fft routines. But the absolute computing time of the MKL routines, in most of the cases, are faster than FFTW.
Have you tested the 3D routines offered by these libraries?
No, I did not yet test 3d FFT performance. Note that FFTW3.x reaches good performance only when run in measure-mode. According to my tests FFTW (in measure-mode) and MKL perform similar (on single data sets). Depending on the problem size and the hardware FFTW3.x or MKL may be slightly faster than the other. An important use-case where MKL shows some performance issues was presented in the blog post above.
Heiko, thank you for this post! It was great to know that FFTW outperforms MKL for large transforms. I’d like to share an interesting detail about the parallel scalability. For our problem, we had to compute a number of large independent 1D FFTs, and we did not have enough RAM in our 40-core system to run 80 or 40 concurrent single-threaded processes. I was curious how much performance I will lose by running, for example, ten 8-threaded instead of eighty 1-threaded concurrent FFTs, and found your post. When I originally looked at the result for N=2^13, I thought “wow, a speedup of 3 with 8 threads? FFTW does not scale well at all!”. However, later I realized that there is an important difference between running a single multi-threaded FFT process on the machine and running several independent multi-threaded FFT processes concurrently to keep the machine fully loaded. With the machine under full load, single-threaded FFTs are slower than when there is just one single-threaded process running. And, therefore, the loss in performance from multi-threading in concurrent transforms is very insignificant (at least, for the large transform sizes that I tested). If it is of any relevance to you, here is a link to the study (PDF file linked therein): http://research.colfaxinternational.com/post/2012/02/02/FFTW-NUMA.aspx
Since you used omp_set_num_threads() it might not do anything if you have MKL_NUM_THREDS or MKL_DOMAIN_NUM_THREADS in your environment variables. Thus you should use mkl_set_num_threads() for the MKL timings.
May i see your Intel MKL FFT test code?Thank you very much.
It’s the code shown my post plus a wrapper library that comes with MKL. With this wrapper libray it is possible to use the FFT routines of MKL as a dropin replacement fro FFTW3.
Hi!
I’m writing very similar source and I’ve got a problem: When I use fftw_plan_with_nthreads() function, time of running programme is 32-times more longer than for 1 thread. Do you have any idea why is that?